Wednesday, December 17, 2014
Hour of Code
This week's project was really one of the weirdest and most confusing projects I have ever been told to do. But at the same time, challenging and fun. It was new at first and when i opened the website thought it was the wrong address because it looked like a child's website but I was wrong (unless those children are like super super smart). The thing that was most challenging was trying to remember all of the different patterns and rules that i learned...not even three slides before. I learned overtime how to use reasoning and remember patterns. I enjoyed the game, like winning the game. Not drowning or hitting the walls. But the surprise thing was that, that really helped my understanding of how Reasoning works.
Wednesday, November 5, 2014
This Year
Three things I have learned this year is:
One thing that could make this class better is having more of a quiet enviornment.
One thing im always proud of is the work i turn in.
- How to work for the things i want.
- How to manage my time wisely.
- What commitment really means, not only for school but with extra curricular activities.
One thing that could make this class better is having more of a quiet enviornment.
One thing im always proud of is the work i turn in.
Tuesday, October 7, 2014
Cut By a Transversal
Parallel Lines Non-Parallel Lines:

Not having parallel lines and splitting them with a transversal would throw off your data. You'd think that something would be true when it's not. You would be able to use the Theorems with regular parallel lines but when they aren't parallel you don't know what formulas to use, if any! Using parallel lines just simplify all your work. While Non-Parallel line make them more difficult than it should be.
Not having parallel lines and splitting them with a transversal would throw off your data. You'd think that something would be true when it's not. You would be able to use the Theorems with regular parallel lines but when they aren't parallel you don't know what formulas to use, if any! Using parallel lines just simplify all your work. While Non-Parallel line make them more difficult than it should be.
Tuesday, September 30, 2014
Practice A Theorems
Theorem 3.1:
All right angles congruent.

Theorem 3.2:
If two lines are perpendicular, then they intersect too form four right angles.

Theorem 3.3:
If two lines intersect to form adjacent angles, then the lines are perpendicular.

Theorem 3.4:
If two sides of adjacent acute angles are perpendicular, then the angles are complementary.

All right angles congruent.
Theorem 3.2:
If two lines are perpendicular, then they intersect too form four right angles.
Theorem 3.3:
If two lines intersect to form adjacent angles, then the lines are perpendicular.
Theorem 3.4:
If two sides of adjacent acute angles are perpendicular, then the angles are complementary.
Tuesday, September 23, 2014
Linear Pair and Vertical Angles
Linear Pairs are a group of non adjacent angles that equal up to 180 degrees. Linear Pairs lie on the same line and are split (not always in half).

Vertical Angles are always congruent and opposite of each other. They are share a vertex and can be more or less than 180 degrees. It doesn't matter how many lines split the figure, as long as there are two or more lines intersecting then there are always Vertical Angles.
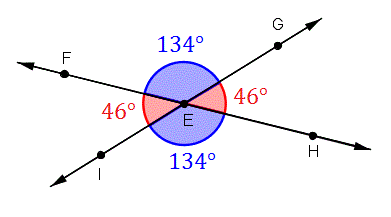
Vertical Angles are always congruent and opposite of each other. They are share a vertex and can be more or less than 180 degrees. It doesn't matter how many lines split the figure, as long as there are two or more lines intersecting then there are always Vertical Angles.

Thursday, September 18, 2014
Law of Syllogism
The Law of Syllogism is when there are two hypothesis and conclusion statements and you put them together.There is one topic with two separate statements in them, and you combine the hypothesis statement from the first sentence and the conclusion from the second sentence.
Example:
If I'm 6'2, then I am tall,
if i am tall, then i can see over people.
So the syllogism of those statements are - If I'm 6'2, then i can see over people.

Example:
If I'm 6'2, then I am tall,
if i am tall, then i can see over people.
So the syllogism of those statements are - If I'm 6'2, then i can see over people.

Wednesday, September 10, 2014
Question ! Page 70
Complementary angles equal 90 degrees and are located on the edge. While supplementary angles are located on the side and equal 180 degrees.
CA=90 degrees
SA=180 degrees
I learned that supplementary angles are located on the side and that complementary angles are located on the corner.
CA=90 degrees
SA=180 degrees
I learned that supplementary angles are located on the side and that complementary angles are located on the corner.
Sunday, September 7, 2014
How Many Handshakes?
If there are 3 to 5 people in one group of people trying to handshake each other, the results may vary. With 3 people in one group you can have 3 handshakes. With 4 people you can can have 6 handshakes. And with 5 people you can have 10 handshakes. In the end you'll get 10 handshakes (max) from 5 people in one group. The way to do this experiment is by getting 3-5 group members and try to handshake as many other group members as you can without handshaking a single person twice and once you reach your max, that's how many handshakes you can have. The function rule to finding out how many handshakes can take place with a certain amount of time is F(n)= n(n-1) .
2


2

Why Math?!?
There is only math because God said so. There are many ways to think about why there is math today and one of the "doorways" to that conversation is through spiritual/philosophical thinking. In Genesis 1:28 God says "be fruitful and multiply; fill the earth and subdue it; have dominion over the fish of the sea, over the birds of the air; and over every living thing that moves on the earth." And there are many things you can take away from this, but what I took from this in a mathematical point of view is that it takes more than one (thing/person) to increase and in looking at this we see that God used a mathematical term , multiply, so as I think about how math came to be, maybe that's why/how. And in this case two people reproducing to multiply population. Another doorway is personal. And math could be helpful in many, if not all things you do, for example: Being fruitful and multiplying. And being practical there is math to help define things or help find an answer that someone might not see.
Thursday, September 4, 2014
Hello World!!!!
Hey I'm Myles Belyeu. Right now the three most important things to me are: 1)God 2) family and 3) sports. This year I'm excited about coming to a new environment, making new friends, and becoming more successful while preparing myself for the future. But at the same time I'm anxious about not being fully prepared for this school. Coming from a normal public school, the teachers don't teach you anything to prepare anyone for anything that is to come in life, and now that I'm in a new school that requires more from me, I'm hesitant about what may come. One thing you might not know about me, (going back to sports) is that I have gone to 12 National Championships and won 9 of them.
Subscribe to:
Comments (Atom)